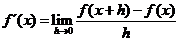DERIVADAS
El estudio de uno de los conceptos fundamentales del
cálculo diferencial es la derivada de una función.
El
otro concepto es la antiderivada o integral; ambos conceptos están relacionados
por el teorema fundamental del cálculo.
Es
de capital importancia dominar la derivación para después poder abordar el
trazado de curvas, así como para comprender a manejar el cálculo integral.
La
derivada de una función en un punto "a" surge del problema de
calcular la tangente a la gráfica de la función en el punto de abscisa
"a", y fue Fermat el primero que aportó la primera idea al tratar de
buscar los máximos y mínimos de algunas funciones. En dichos puntos las
tangentes han de ser paralelas al eje de abscisas, por lo que el ángulo que
forman con éste es de cero grados. En estas condiciones, Fermat buscaba aquellos
puntos en los que las tangentes fueran horizontales
La
derivada de una función en un punto mide, por tanto, la pendiente de la
tangente a función en dicho punto. Nos va a servir para estudiar el crecimiento
o decrecimiento de una función o la concavidad o convexidad de la misma en los
diferentes intervalos en los que se puede descomponer su campo de existencia.
Es importante tener en cuenta que hay funciones que no tienen derivadas en un punto, y que para que una función tenga derivada, la función debe ser continua pero no todas las funciones continuas son derivables en todos sus puntos
Es importante tener en cuenta que hay funciones que no tienen derivadas en un punto, y que para que una función tenga derivada, la función debe ser continua pero no todas las funciones continuas son derivables en todos sus puntos
La derivada de la función f(x) en
el punto x = a es el valor del límite, si existe, de un cociente incremental
cuando el incremento de la variable tiende a cero.
- Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define la derivada en el punto "a" como:
- Sí en lugar de considerar h el incremento de la variable independiente x lo sustituimos por Δx tenemos que la definición queda:
- En el caso de que hagamos h=x-a tenemos a+h=x, y la definición nos queda de la siguiente forma:
- Función derivada. Dada la función f(x) continúa en el intervalo abierto I denominamos función derivada a:
- Sí en lugar de considerar h el incremento de la variable independiente x lo sustituimos por Δx tenemos que la definición queda:
1. Hallar
la derivada de la función f(x) = 3x2 en el punto x = 2.
2. Calcular
la derivada de la función f(x) = x2 + 4x − 5 en x = 1.
REGLAS DE DERIVACIÓN
REGLAS DE DERIVACIÓN (CONTINUA)
IMPORTANCIA DE LAS DERIVADAS
La derivada permite ver, a través de la pendiente en todo
punto de la curva, la evolución o el cambio de muchos fenómenos físicos. Permite
calcular los puntos clave ahí donde la pendiente es 0 (máximos y mínimos) para
buscar los óptimos por ejemplo. Permite hacer otros muchos cálculos asociados a
este hecho de la pendiente de la tangente en cada punto de la curva. En física,
electricidad, electrónica, en química, permite estudiar muchos fenómenos
evolutivos asociados como la velocidad, la aceleración, los flujos, las
acumulaciones. Las derivadas están siempre presentes. Se utiliza en economía,
se utiliza en gestión, se utiliza en arquitectura. Los sistemas de cálculo de
frenado y de automatización utilizan derivadas, los sistemas y las máquinas
automatizadas para fabricar o para controlar utilizan derivadas. Por ejemplo,
los sistemas que controlan la parada de vuestro ascensor para que ésta sea
suave, se controla el “jerk” que es la derivada de la aceleración con relación
al tiempo.
EJEMPLO DE TRAYECTORIA DEL ASCENSOR USO DE
LA DERIVADA (JERK)
Posicionamiento
con NIVELACIÓN a planta
Posicionamiento
DIRECTO en la planta
Posicionamiento
para planta CORTA
Asimismo cuando queremos trasladar un auto por estas
escaleras hacia arriba
Dispones de unos tablones que irás poniendo de peldaño a
peldaño (Figura 2) para poder desplazar tu carro
Fíjate
en ellos, observa la figura 2 ¿Qué constatas con relación a su inclinación?
Tendrás
que hacer mucho esfuerzo al inicio para desplazar tu carro y menos al final en
el último tramo. La pendiente, aunque subas todo el tiempo, es más elevada al
inicio que al final.
Si establecemos
el ángulo entre el tablero y la horizontal (Figura 3), vemos que el ángulo se
va reduciendo a medida que vamos avanzando a lo largo de los tablones. Se dice
que el coeficiente director de la pendiente va reduciéndose.
Por
ejemplo, en el punto 6, o 7, o 8, y 9 (el tablero azul) tenemos una pendiente
con un coeficiente director de ¼ ya que tiene que recorrer 4 unidades de medida
(la profundidad de la escalera) para subir 1 unidad en el punto 10 (altura de
la escalera). La pendiente es la división de lo que ha subido (1 punto) sobre
lo que ha avanzado (4 unidades), es decir la pendiente es de 1/4= 0,25 (es lo
que se llama el coeficiente director de la recta). La pendiente del tablero
amarillo, es de 0,2, ya que hay que recorrer 5 para subir 1. Si, por ejemplo en
este mismo punto, en lugar de una unidad se subiese 10 unidades ¿Cuál sería la
pendiente en este caso?
La
pendiente en ese caso sería de 10/5= 2.
APLICACIÓN DE LAS DERIVADAS EN LA
ARQUITECTURA
En el campo de las construcciones, los arquitectos,
ingenieros y profesionales de estas áreas usualmente emplean la integral para
obtener el área de superficies irregulares; áreas y volúmenes de regiones y
sólidos de revolución es decir de cilindros, conos, etc. Y las derivadas para
determinar el límite.
Podemos apreciar el uso de integrales y derivadas en
construcciones, diseños de túneles, estadios, edificios, cúpulas y otras
superficies que tengan formas irregulares; curvas, ovaladas, elipses,
parábolas, hipérbolas, etc.
El ’56 Leonard Street’ de Tribeca, la torre residencial más original diseñada en Manhattan, Nueva York
Otro ejemplo es el restaurante “Los Manantiales” del parque de
Choximilco en la ciudad de México. El techo está formado por ocho paraboloides
hiperbólicos. Las matemáticas a través de dimensiones y formas el diseño del
edificio y le confieren una belleza aceptada universalmente.El ’56 Leonard Street’ de Tribeca, la torre residencial más original diseñada en Manhattan, Nueva York
’56
Leonard Street’ de Tribeca
Los Manantiales
BIBLIOGRAFÌA